Probability & Statistics Fundamentals: Part I
Disclaimer: The notes and images from this post were taken from the books/works listed in the References section. The intention of this post is to provide a summary of Probability & Statistics.
Random Variables
A random variable can be seen as the name of an experiment with a probabilistic outcome. It’s value is the outcome of that experiment - Tom Mitchell, 1997
Definitions:
Definition 1:
A random variable is a function that assigns a real number to each outcome in the sample space of a random experiment [1].
Definition 2:
For a given sample space $\mathcal{S}$ of some experiment, a random variable (rv) is any rule that associates a number with each outcome in $S$. In mathematical language, a random variable is a function whose domain is the sample space and whose range is the set of real numbers [2].
A random variable is denoted by an uppercase letter such as $X$. After an experiment is conducted, the measured value of the random variable is denoted by a lowercase letter such as $x = 70$ milliamperes.
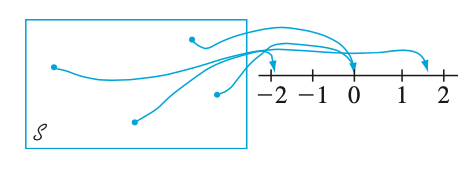
In summary:
-
A discrete random variable is a random variable with a finite range.
-
A continuous random variable is a random variable with an interval of real numbers for its range.
Discrete Random Variable and Probability Distributions
The probability distribution of a random variable X is a description of the probabilities associated with the possible values of X.
For a discrete random variable, the distribution is often specified by just a list of the possible values along with the probability of each. In some cases, it is convenient to express the probability in terms of a formula.
Probability Mass Function
For a discrete random variable $X$, its distribution can be described by a function that specifies the probability at each of the possible discrete values for $X$
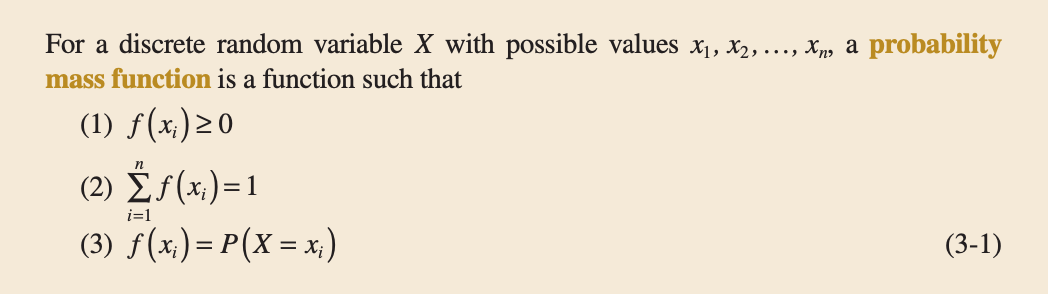
The next Figure, shows an example of a probability mass function:
Cumulative Distribution Functions
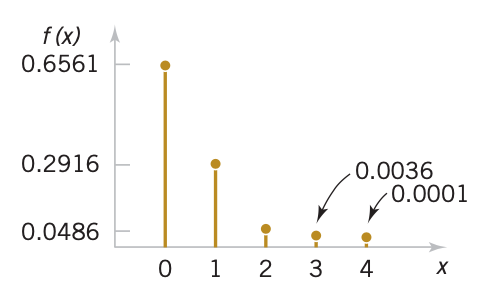
In general, for any discrete random variable with possible values $x_1,x_2,…,$ the events ${X = x_1}, {X = x_2},…$ are mutually exclusive. Therefore, $P(X \leq x) = \sum_{x_i \leq x} P(X = x_i )$. This leads to the following definition:
A cumulative distribution function satisfies the following properties:
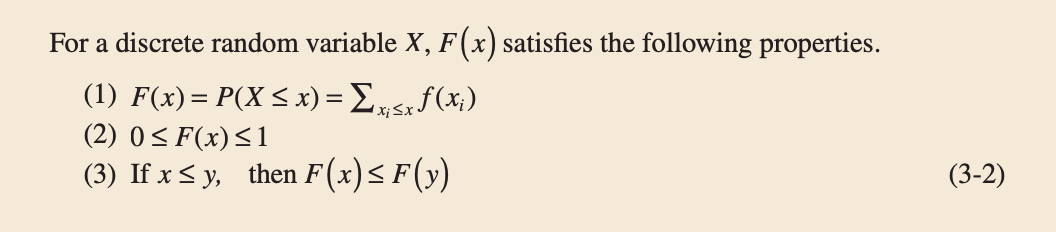
Mean and Variance of a Discrete Random Variable

The mean of a discrete random variable $X$ is a weighted average of the possible values of $X$ with weights equal to the probabilities. If $f(x)$ is the probability mass function of a loading on a long, thin beam, $\mathbb{E}(X)$ is the point at which the beam balances. Consequently, $\mathbb{E}(X)$ describes the “center” of the distribution of $X$ in a manner similar to the balance point of a loading.
The variance of a random variable $X$ is a measure of dispersion or scatter in the possible values for $X$. The variance of $X$ uses weight $f(x)$ as the multiplier of each possible squared deviation $(x − \mu)^2$. The variance of a random variable $X$ can be considered to be the expected value of a specific function of $X$, namely, $h(X)= (X − \mu)^2$.
In general, the expected value of any function $h(X)$ of a discrete random variable is defined in a similar manner.
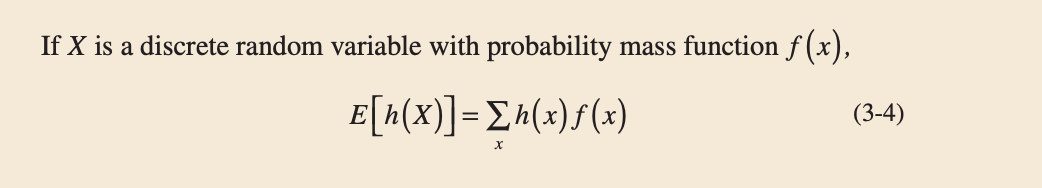
Continuous Random Variable and Probability Distributions
A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
Because the number of possible values of $X$ is uncountably infinite, $X$ has a distinctly different distribution from the discrete random variables.
Probability Density Function
A probability density function $f(x)$ can be used to describe the probability distribution of a continuous random variable $X$. If an interval is likely to contain a value for $X$, its probability is large and it corresponds to large values for $f(x)$. The probability that $X$ is between $a$ and $b$ is determined as the integral of $f(x)$ from $a$ to $b$.
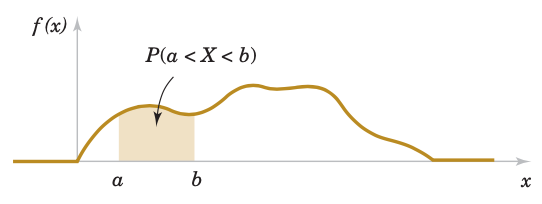
A probability density function (pdf) provides a simple description of the probabilities associated with a random variable. A pdf is zero for x values that cannot occur, and it is assumed to be zero wherever it is not specifically defined.
The important point is that $f(x)$ is used to calculate an area that represents the probability that $X$ assumes a value in $[a, b]$

Cumulative Distribution Functions
An alternative method to describe the distribution of a continuous random variable can also be use in the same way as for discrete random variables. The cumulative distribution function is defined for all real numbers.
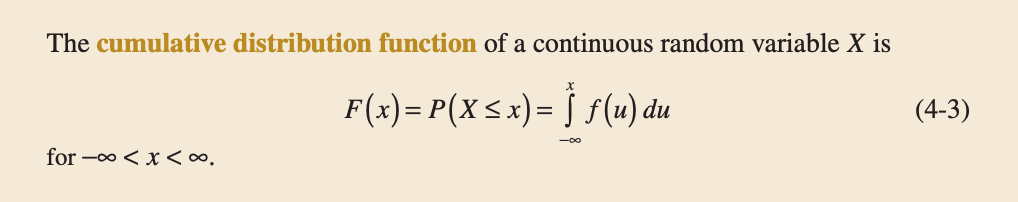
The probability density function of a continuous random variable can be determined from the cumulative distribution function by differentiating. The fundamental theorem of calculus states that
\[\begin{equation} \frac{d}{dx}\int_{-\infty}^{x}f(u)du = f(x) \end{equation}\]
Mean and Variance of a Continuous Random Variable
For a continuous random variable, integration replaces summation used in the discrete definitions.

The expected value of a function $h(X)$ of a continuous random variable is also defined in a straightforward manner.
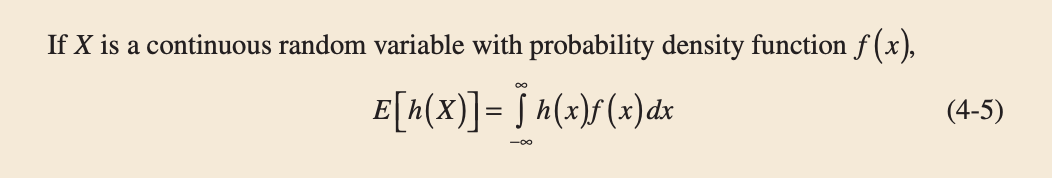
In the special case that $h(X) = aX+b$, for any constants $a$ and $b$, $\mathbb{E}[h(X)] = a \; \mathbb{E}(X)+ b$. This can be shown from the properties of integrals.
References
-
MONTGOMERY, Douglas C.; RUNGER, George C. Applied statistics and probability for engineers. John Wiley & Sons, 2010.
-
DEVORE, Jay L. Probability and Statistics for Engineering and the Sciences. Cengage learning, 2011.
If you found this useful, please cite this as:
Arnez Yagualca, Fabio Alejandro (Apr 2020). Probability & Statistics Fundamentals: Part I. Fabio Arnez - Website. https://FabioArnez.github.io.
or as a BibTeX entry:
@article{arnez yagualca2020probability-statistics-fundamentals-part-i,
title = {Probability & Statistics Fundamentals: Part I},
author = {Arnez Yagualca, Fabio Alejandro},journal = {Fabio Arnez - Website},
year = {2020},
month = {Apr},
url = {https://FabioArnez.github.io/blog/2020/Probability-Statistics-Fundamentals-I/}
}
Enjoy Reading This Article?
Here are some more articles you might like to read next: